CUTLASS-Cute 初步(1)：Layout

• github – Layout 测试代码

Cute(CUDA Tensor) 是 CUBLASS 扩展，用于简化张量 BLAS 操作和内存布局的管理。

最主要的概念是 Tensor 和 Layout：

• Layout<Shape, Stride>: 定义张量的内存布局，用于将一维内存地址映射到多维张量索引。
  • Shape：Logical dimensions，张量的逻辑维度/形状。
  • Stride：Physical steps，每一个维度在内存中的步长/跨度。
• Tensor<Engine,Layout>: 定义张量的数据类型/存储和布局。

映射公式：

offset = Σ (index[i] * stride[i])

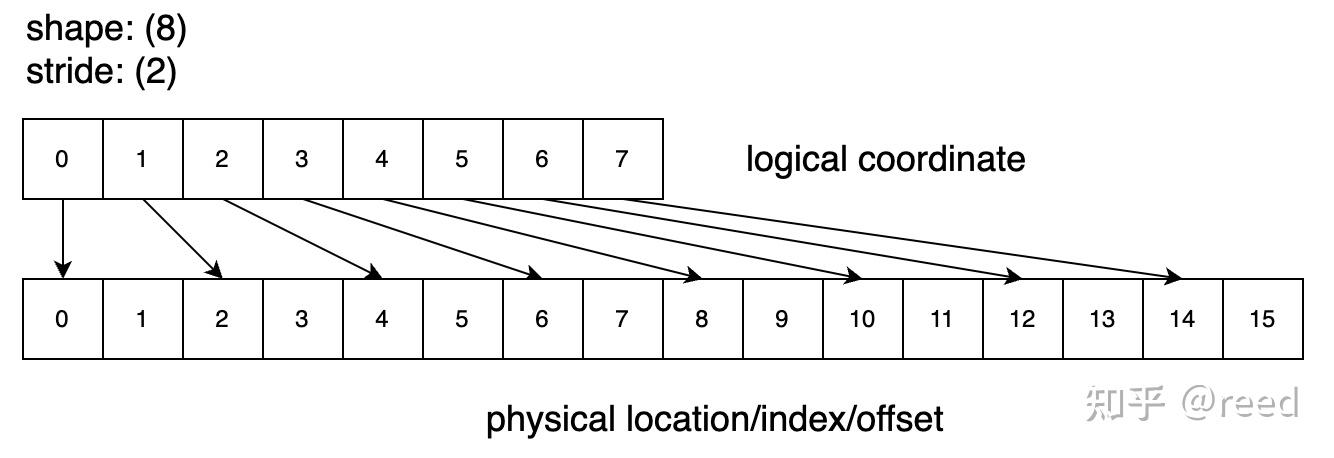
Layout 本质是一个映射函数，将多维索引映射到一维内存地址。称索引为定义域(domain)，映射得到的地址为值域(codomain)。以一个一维映射为例：

如上图 layout (8):(2)，按照映射公式得到 index_phy = index_logic * 2，将连续以一维索引 0,1,2,…7 映射到内存地址 0,2,4,…14。此时：

• size(layout) = 8
• cosize(layout) = 16

而如果定义 layout (8):(0)，则所有逻辑索引都映射到内存地址偏移 0，即所有索引映射到同一个地址。此时得到：

• size(layout) = 8
• cosize(layout) = 1

1. Layout 示例

1.1. 例一：定义一个两行三列的矩阵布局，这个矩阵采用列主序存储

    auto tensor_shape = make_shape(2, 3);   // 两行三列
    auto tensor_stride = make_stride(1, 2); // 列主序存储
    auto tensor_layout = make_layout(tensor_shape, tensor_stride);
    print_layout(tensor_layout);

输出：

(2,3):(1,2)
      0   1   2
    +---+---+---+
 0  | 0 | 2 | 4 |
    +---+---+---+
 1  | 1 | 3 | 5 |
    +---+---+---+

// A(m, n) = storage[m*1 + n*2]
const auto val = tensor_layout(1, 2); // 访问张量元素 (1,2)，值为 5

1.2. 例二：定义一个两行三列的矩阵，这个矩阵采用行主序存储

    auto tensor_shape = make_shape(2, 3);   // 两行三列
    auto tensor_stride = make_stride(3, 1); // 行主序存储
    auto tensor_layout = make_layout(tensor_shape, tensor_stride);
    print_layout(tensor_layout);

输出：

(2,3):(3,1)
      0   1   2
    +---+---+---+
 0  | 0 | 1 | 2 |
    +---+---+---+
 1  | 3 | 4 | 5 |
    +---+---+---+

1.3. 例三：定义一个三维张量布局

• 张量形状：(4,2,2)，dim0=4, dim1=2, dim2=2
• 张量步长：(4,1,2) 行主序存储，子 tensor 为列主序

    auto tensor_shape = make_shape(4, make_shape(2, 2));
    auto tensor_stride = make_stride(4, make_stride(1, 2));
    auto tensor_layout = make_layout(tensor_shape, tensor_stride);
    print_layout(tensor_layout);

输出：

    (4,(2,2)):(4,(1,2))
           0    1    2    3
        +----+----+----+----+
     0  |  0 |  1 |  2 |  3 |
        +----+----+----+----+
     1  |  4 |  5 |  6 |  7 |
        +----+----+----+----+
     2  |  8 |  9 | 10 | 11 |
        +----+----+----+----+
     3  | 12 | 13 | 14 | 15 |
        +----+----+----+----+

// A(i, (j, k)) = storage[i*4 + j*1 + k*2]
const auto val1 = tensor_layout(2, make_coord(1, 0)); // 访问张量元素 (2,(1,0))，值为 9

1.4. 例四：定义一个三维张量布局

• 张量形状：(4,2,2)，dim0=4, dim1=2, dim2=2
• 张量步长：(2,1,8)

    auto tensor_shape = make_shape(4, make_shape(2, 2));
    auto tensor_stride = make_stride(2, make_stride(1, 8));
    auto tensor_layout = make_layout(tensor_shape, tensor_stride);
    print_layout(tensor_layout);

输出：

    (4,(2,2)):(2,(1,8))
           0    1    2    3
        +----+----+----+----+
     0  |  0 |  1 |  8 |  9 |
        +----+----+----+----+
     1  |  2 |  3 | 10 | 11 |
        +----+----+----+----+
     2  |  4 |  5 | 12 | 13 |
        +----+----+----+----+
     3  |  6 |  7 | 14 | 15 |
        +----+----+----+----+

// A(i, (j, k)) = storage[i*2 + j*1 + k*8]
const auto val1 = tensor_layout(2, make_coord(1, 0)); // 访问张量元素 (2,(1,0))，值为 5

几何解释：

内存布局（一维）：
[0][1][2][3][4][5][6][7] | [8][9][10][11][12][13][14][15]
 ←───── 块 k=0 ─────→     ←────── 块 k=1 ──────→

Stride 分量	值	含义
stride_i	2	沿 i 方向移动一步，offset 增加 2
stride_j	1	沿 j 方向移动一步，offset 增加 1
stride_k	8	沿 k 方向移动一步，offset 增加 8（跳到另一个块）

关于几何解释，更多理解内容参考帖子 https://note.gopoux.cc/hpc/cute/layout/

1.5. CuTe IntTuple

定义多维 Tensor 时，可以使用嵌套的 Shape 和 Stride 来定义子 Tensor 的形状和步长。在 Cute 中，使用 template tuple 表示表示嵌套的 Shape 和 Stride。

具体是使用 IntTule 表示：IntTuple 可以是一个整形，也可以是一个 tuple，并且可以嵌套。以下都是一个合法的 IntTuple：

• int{3}，运行时整数。
• Int<3>{}，Int<3>() 编译时整数，称为静态整数。另外，定义了一些字面量：比如 _1、_2、_3 分别定义为 Int<1>{}、Int<2>{}、Int<3>{}。
• 带有任何模板参数的 IntTuple，比如 make_tuple(int{2}, Int<3>{})。

在对 layout 进行一些操作时，还定义了一些常量表示这些操作：

• cute::_ : 获取 slice 时，表示或者这个维度（轴）的所有数据，在 Python 中类似于 :。
• cute::X ：在切分操作（比如partition）的时候，表示不对这个维度进行切分。

2. Hierarchy Layout

层级化的 layout 概念用于更加直观的表示多维 tensor，拆分 layout 划分工作，更好的表示内存局部性，如 TV layout。

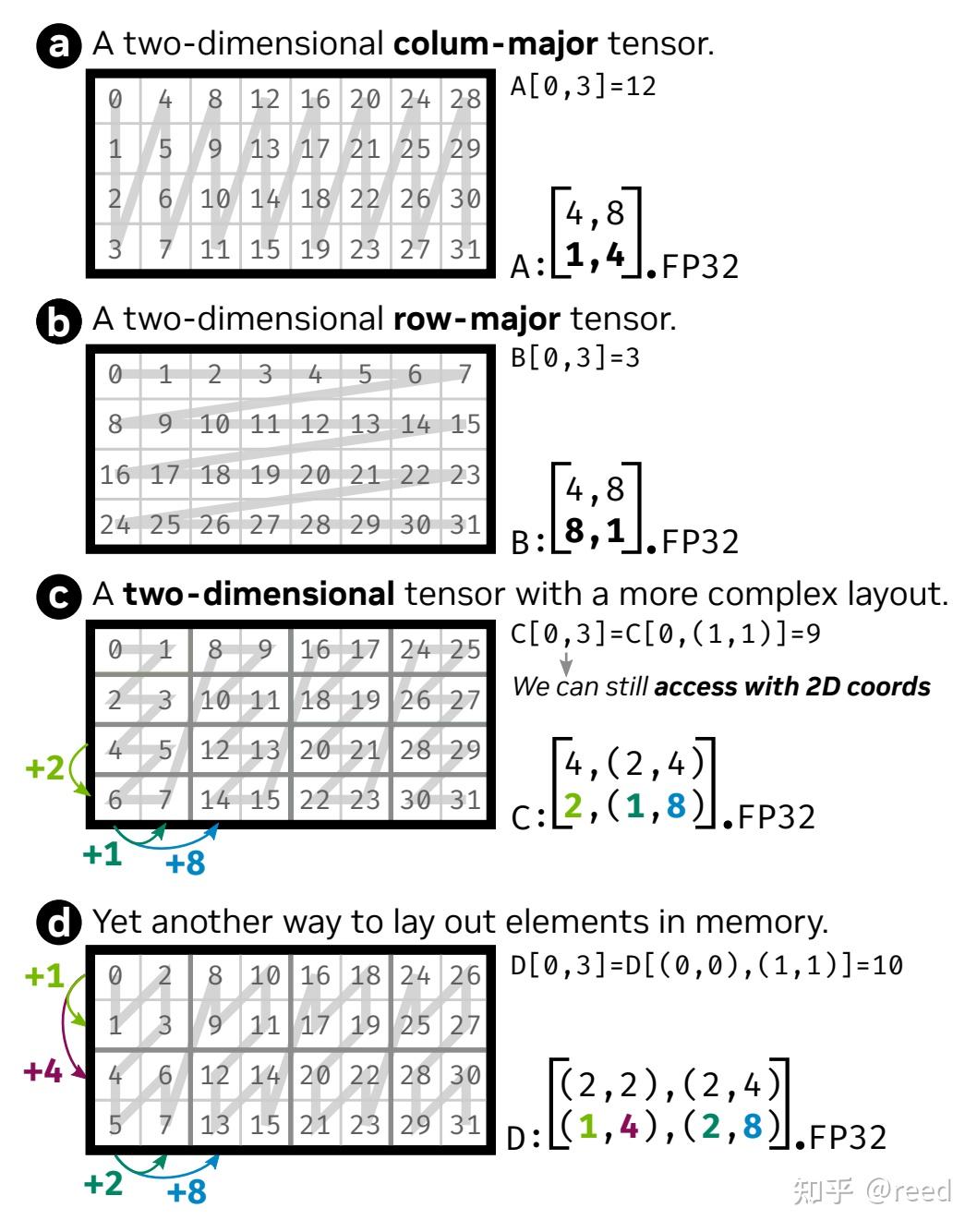
上图示例中，a, b 情形分别表示 column-major 和 row-major 布局的二维矩阵，不存在嵌套。

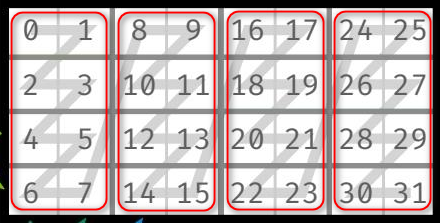
2.1. 嵌套 layout 示例 c

示例 c 中，可以将其看作一个嵌套的 layout：在列方向上存在一个嵌套的 layout。

• 内层 layout （红色框内）为: (4, 2):(2, 1)。
• 外层 layout 为: (1, 4):(4, 1)。即外层 layout 是一个有 1 行 4 列的矩阵（向量），每个元素是一个内层 layout。

合并之后，表示 4 行 8 列。其中，列方向为两个层次：(2, 4)，2 表示内层 layout 的列数，4 表示外层 layout 的列数。

综合起来的 shape 为 (4, (2, 4))，其含义为（按顺序表示）：第一个 4 表示行数，2 表示内层 layout 列数，第二个 4 表示外层 layout 列数。

针对 stride，其表示顺序要与 shape 保持一致，即 如果 shape 为 (sx, (sy, sz))，则 stride 为 (dx, (dy, dz))即 stride(2, (1, 8)) 的含义如下：

• dx：内层 layout 行方向的间隔为 2。注意：这里解读为内层 layout 的行方向间隔，这个 layout 在行方向上没有外层。
• dy：内层 layout 列方向的间隔为 1。
• dz：外层 layout 列方向的间隔为 8，即为一个内层 layout 块的大小。

综合得到 layout 为 (4, (2, 4)):(2, (1, 8))。

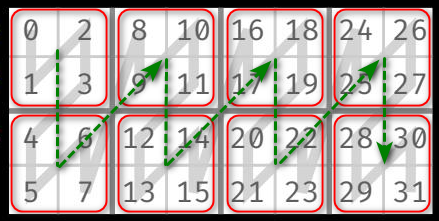
2.2. 嵌套 layout 示例 d

示例 d 的 layout 在行列方向上均存在嵌套 layout。两层 layout 分别为：

• 内层 layout （红色框内）为: (2, 2):(2, 2)。
• 外层 layout 为: (2, 4):(4, 1)。

合并之后，表示 4 行 8 列。其中，行方向为两个层次：(2, 2)，列方向为两个层次：(2, 4)。即：

• ((sx1, sx2):(sy1, sy2))，得到综合 shape 为 ((2, 2), (2, 4))。
  • sx1 表示内层 layout 行数，sx2 表示外层 layout 行数；
  • sy1 表示内层 layout 列数，sy2 表示外层 layout 列数。
• 对应的，综合 stride 为 ((dx1, dx2), (dy1, dy2))，得到((1, 4), (2, 8))。

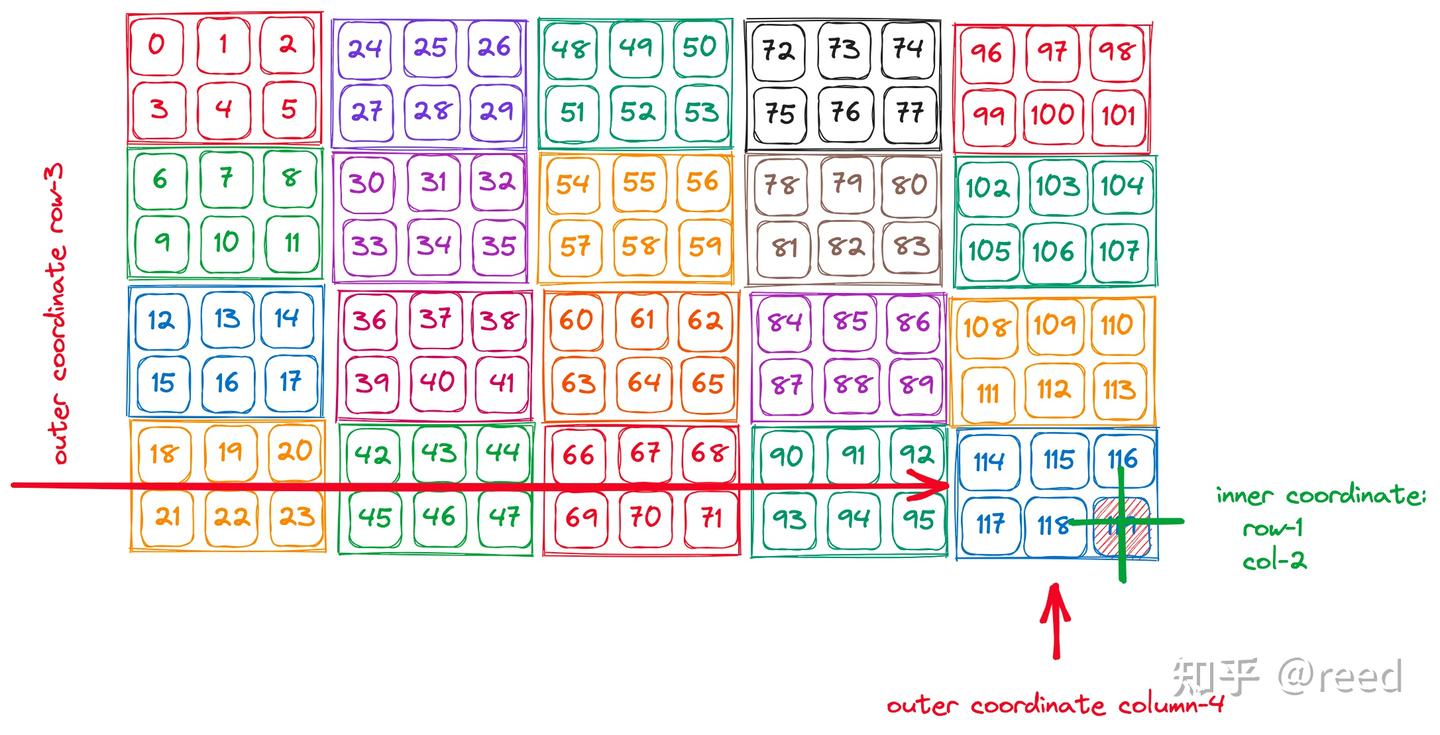
2.3. 坐标及数据访问 coordinate

对一个 layout 为 ((2, 4), (3, 5)):((3, 6), (1, 24)) 的 tensor 进行数据访问时，其访问格式遵从上述的顺序，形式为：

auto row_coord = make_coord(1, 3);
auto col_coord = make_coord(2, 4);
auto coord = make_coord(row_coord, col_coord);

如下图所示：

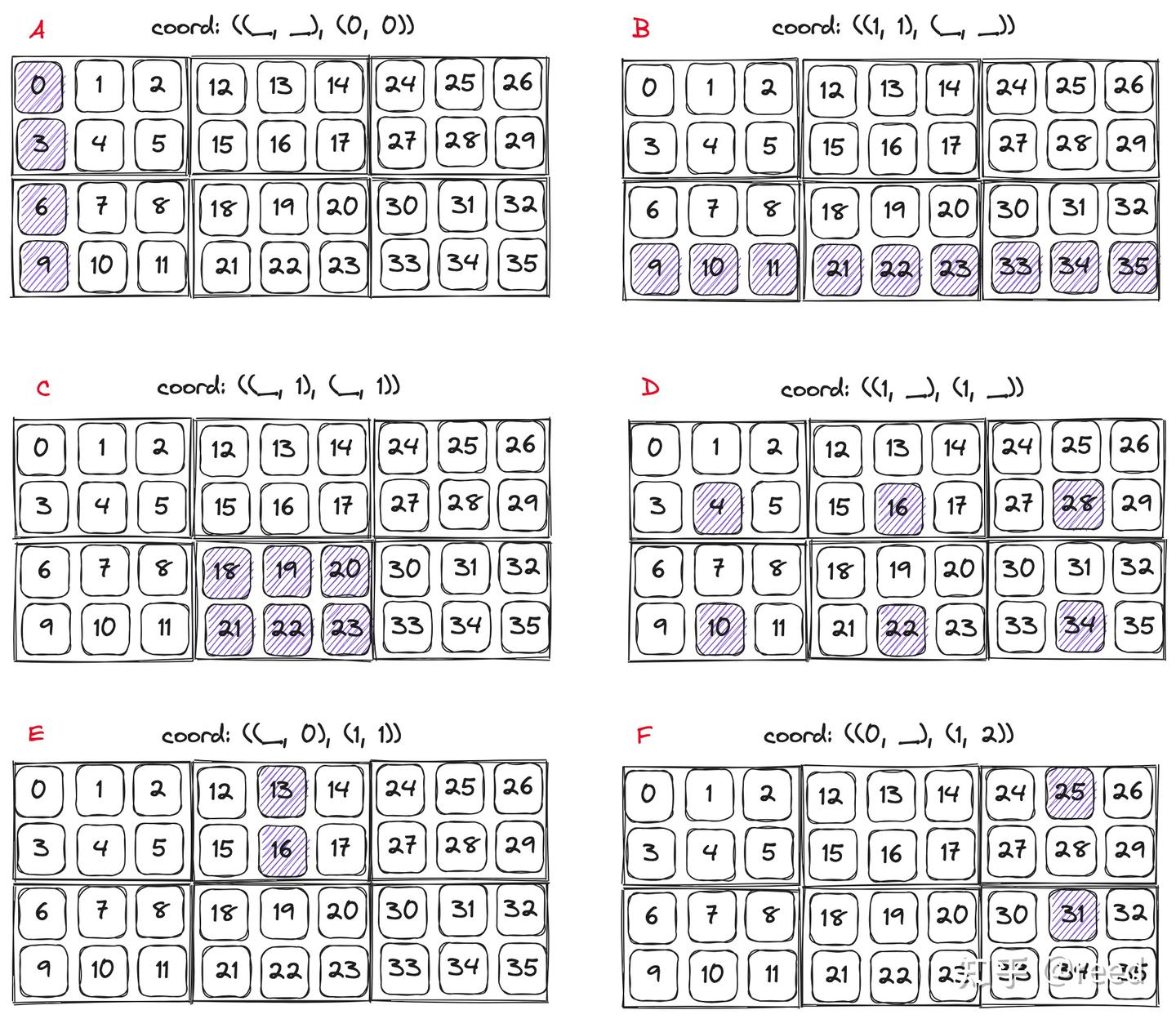
2.4. slice 操作

CuTe 提供了 slice 函数，使用 UnderScore cute::_，用于获取指定维度的子 layout。如下图所示：

使用方式如下：

auto layout = make_layout(
    make_shape(make_shape(2, 4), make_shape(3, 5)),
    make_stride(make_stride(3, 6), make_stride(1, 24))
);

auto row_coord = make_coord(1, 1);
auto col_coord = make_coord(cute::_, cute::_);
auto coord = make_coord(row_coord, col_coord); // 获取子块 B
auto sub_layout = cute::slice(coord, layout);

参考及资料

• reed – cute 之 Layout
• Yifan Yang (杨轶凡) – CuTe Layout and Tensor
• CUTLASS CUTE 1 Layout Algebra