CUTLASS-Cute 初步(2)：Tensor & Layout Algebra

• github – 测试代码
• CuTe Tensors：官方文档

1. CuTe 中的 Tensor 划分 (Partitioning a Tensor)

在 GEMM 计算是，需要对矩阵进行划分（分块），以便线程块（Thread Block）和线程（Thread）能够并行处理数据。常用的有 Inner-Partitioning、Outer-Partitioning，以及 TV-layout-Partition。

1.1. Inner-Partitioning

GEMM 计算，先需要按照 Thread Block 划分为若干 Tile，即给每个 Thread Block 分配一个 Tile。如下所示：

Tensor A = make_tensor(ptr, make_shape(8,24));  // (8,24)
auto tiler = Shape<_4,_8>{};                    // (_4,_8)

Tensor tiled_a = zipped_divide(A, tiler);       // ((_4,_8),(2,3))

在使用 tiler 对 A 进行切分之后，(_4, _8) 是第一个mode（first mode），(2, 3) 是第二个mode（second mode）。

• 第一个 mode (mode 0)：Tile 的 shape
• 第二个 mode (mode 1)：Tile 在全局中的排列

mode 是张量代数（tensor algebra）中的一个概念，表示张量的不同维度，或者叫逻辑轴。为了避免与 tensor 中的维度（dimension）混淆，故使用不同的术语。

沿着第二个mode 切分之后，可以得到 2x3 个 Tile，每个 Tile 的 shape 是 4x8：

Tensor cta_a = tiled_a(make_coord(_,_), make_coord(blockIdx.x, blockIdx.y));  // (_4,_8)

由于保留了内部 tile 的 shape 信息，这种切分方式叫做 Inner-Partitioning。CuTe 使用 inner_partition(Tensor, Tiler, Coord) 函数来实现内部分块，在实际使用时，则使用另外一个代替的函数 local_tile(Tensor, Tiler, Coord)来进行 tile 划分（分配给 Thread Block）。

1.2. Outer-Partitioning

在 Thread Block 划分好 tile 之后，下一步就是将 sub-tile 分配给线程（Thread）：

Tensor thr_a = tiled_a(threadIdx.x, make_coord(_,_)); // (2,3)

这一步叫做 Outer-Partitioning，因为这种划分方式对 tile 进行划分，保留了分块的 shape 信息。在 CuTe 中，使用 outer_partition(Tensor, Tiler, Coord) 函数来实现外部分块，在实际使用时，则使用另外一个代替的函数 local_partition(Tensor, Layout, Idx) 来进行 sub-tile 划分（分配给 Thread）。

2. Layout Algebra

2.1. Coalesce：Layout 展平为一维

一些二维的 layout，其二维索引 (m, n) 可以转换得到对应的一维索引 k。例如：

layout (M, N) : (1, M)
k = m + n * M

例子：

auto layout = Layout<Shape<_2,Shape <_1,_6>>,
                     Stride<_1,Stride<_6,_2>>>{};
auto result = coalesce(layout);    // _12:_1

有三种情况可以展平：

• (s0, _1) : (d0, d1) => s0 * d0。忽略第二维的 stride。
• (_1, s1) : (d0, d1) => s1 * d1。忽略第一维的 stride。
• (s0, s1) : (d0, d1) => s0 + s1 * d0。当 d1 == d0 * s0 时，可以展平为一维。

其他情况不能展平为一维 layout，比如 layout codomain 出现空洞，即不是连续映射的。

在 CuTe 中，以一个二维 layout 为例，可以使用layout(m, n) 索引的形式访问，也可以使用 layout(k) 的形式访问。使用一维索引 k 访问时，其应该等于使用 coalesce 展平后的 layout 进行访问。见https://github.com/NVIDIA/cutlass/blob/main/test/unit/cute/core/coalesce.cpp。

2.1.1. By-mode Coalesce：展平部分轴

例如 layout ` ((M, N), K, L) : ((1, M), M * N, M * N * K)，希望展平子 layout (M, N):(1, M)`，保持其他轴的 shape 不变：

coalesce(layout, Step<_1, _1, _1>{});

Step<_1, _1, _1> 表示展平为三维的 layout，因为这个 Step<> 的 rank 是 3。CuTe 对每个轴重新计算，得到新的 layout：

((M*N), K, L) : (1, M*N, M*N*K)

一个完整的例子：

// Coalesce within each top-level mode
auto layout = make_layout(make_shape(Int<2>{}, make_shape(Int<1>{}, Int<6>{})),
                          make_stride(Int<1>{}, make_stride(Int<6>{}, Int<2>{})));
// layout is (2,(1,6)):(1,(6,2))

auto result = coalesce(layout, Step<_1,_1>{});  // result is (2,6):(1,2)
// Coalesced within each mode, preserving rank-2 structure

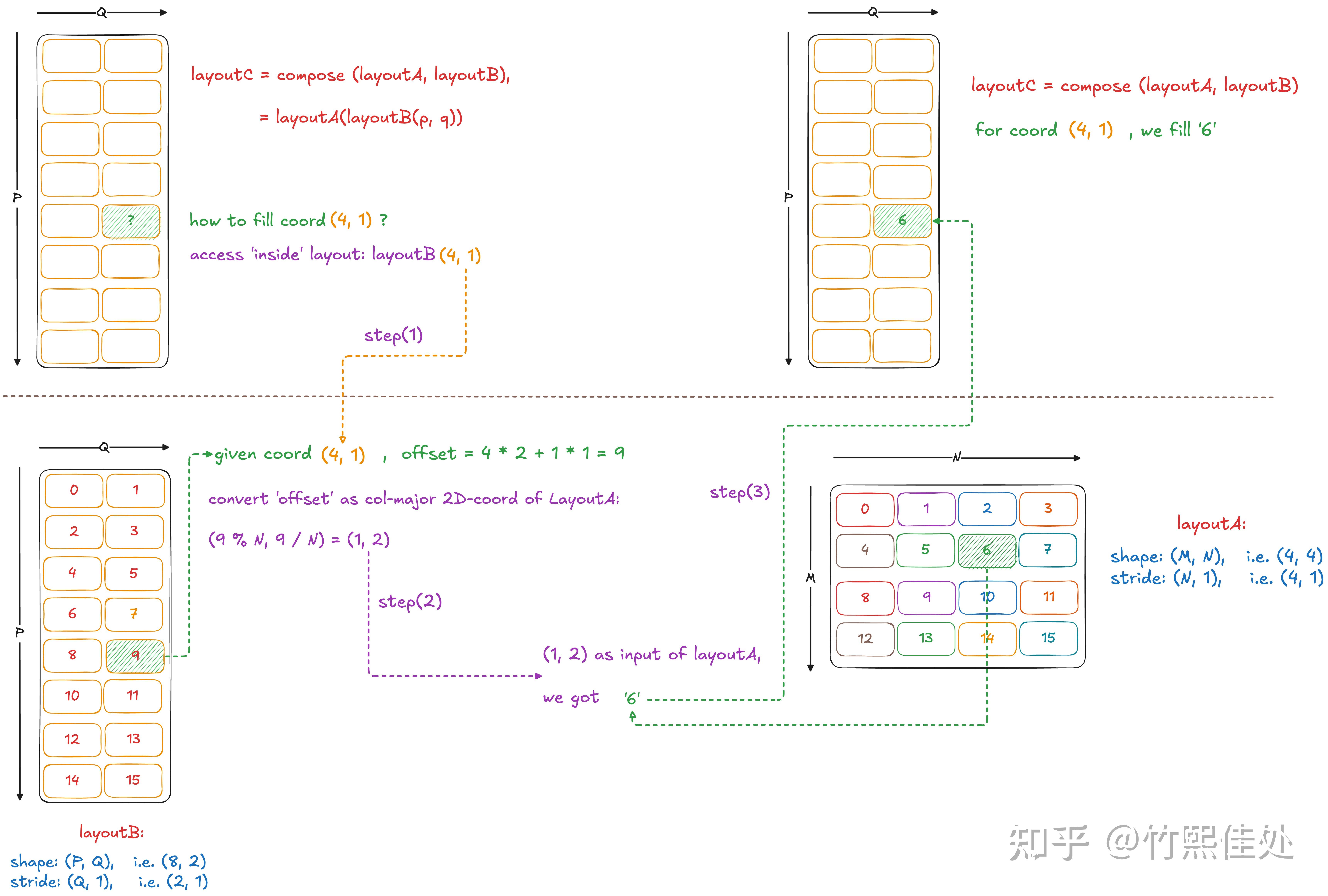
2.2. Composition：Layout 复合

首先，Layout 本质就是一个映射函数，Composition 即经过多次映射：

R(c) := (A o B)(c) := A(B(c))

计算过程如下：

composition 有如下属性：

• 兼容性：compatible(B, R) - B的每个坐标都可以用作R的坐标，因为B定义了R的定义域
• 函数等价性：对于B定义域内的所有i，R(i) == A(B(i))。官方测试用例test composition

2.2.1. By-mode Composition

composition 函数提供一个重载版本，第二个参数为 tiler，对部分维度（轴）进行复合操作。Tiler 可以是：

• 一个 Layout
• Tiler tuple
• Shape，会被解释为步长为 1 的 Tiler

2.2.2. Composition：reshape & reordering

Reshape

// 20-element layout with stride 2
auto layout_1d = make_layout(Int<20>{}, Int<2>{});  // 20:2

// Reshape to 5x4 row-major
auto tiler = make_layout(make_shape(Int<5>{}, Int<4>{}),
                         make_stride(Int<4>{}, Int<1>{}));  // (5,4):(4,1)

auto result = composition(layout_1d, tiler);  // (5,4):(8,2)
// Maps (i,j) coordinates to layout_1d using tiler pattern

结果如下（下左为 tiler，下右为 result）：

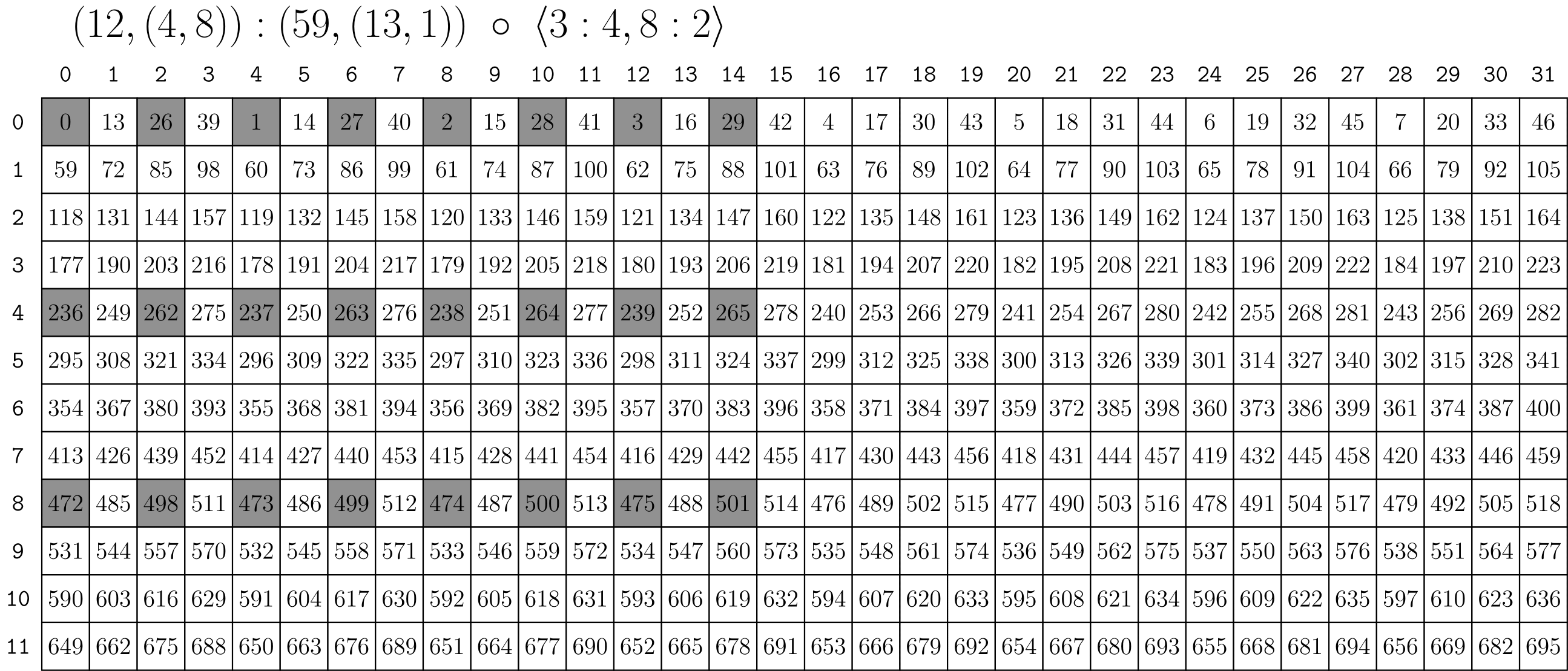
Extract Subtile

// (12,(4,8)):(59,(13,1))
auto a = make_layout(make_shape (12,make_shape ( 4,8)),
                     make_stride(59,make_stride(13,1)));
// <3:4, 8:2>
auto tiler = make_tile(Layout<_3,_4>{},  // Apply 3:4 to mode-0
                       Layout<_8,_2>{}); // Apply 8:2 to mode-1

// (_3,(2,4)):(236,(26,1))
auto result = composition(a, tiler);

结果如下：

参考:

• CuTe Layout and Tensor Tutorial：deepwiki algegra 使用示例解析
• CuTe Layout Algebra：deepwiki algebra 解析
• cute_layout_algebra.ipynb：官方 CuteDSL notebook

学习参考资料

• CuTe Layout Algebra。官方文档
• deepwiki – cutlass – Layout Algebra
• cute Layout 的代数和几何解释。来自知乎 reed 文章
• CuTe Layout and Tensor。来自Yifan Yang (杨轶凡) 博客

三方学习测试代码：

• github – code for layout algebra

其他资料

• A Generalized Micro-kernel Abstraction for GPU Linear Algebra：NVIDIA PPT
• Algebra – 2.12 Inverses and composition：数学理论：composition
• Categorical Foundations for CuTe Layouts
• Layout Algebra：三方实现的C++ Layout Algebra库
• 将 SVG 合并到 SVG：工具：合并svg图片