GEMM优化1：使用 CuTe 实现一个 naive GEMM

发表于 2025/02/26

作者 Roderick.Huang

17 分钟阅读

1. navie tile GEMM

代码文件：navie tile GEMM

基于分块矩阵乘法的简单实现，按照 Thread Block 将矩阵划分为多个tile进行计算，在 Thread Block内，再次将 tile 划分为多个子块，由每个线程负责计算子块。

使用 Shared Memory 来缓存 tile 数据，减少全局内存访问次数。每个线程负责从全局内存中复制 tile 内的一小块内存到 Shared Memory。

循环展开#pragma unroll优化加载和计算部分的循环，提高指令级并行性（消耗更多寄存器资源），本代码测试整体运行时间提升15%左右。

2. CuTe 版本 naive tile GEMM

代码文件：CuTe naive tile GEMM

使用 CuTe 库重写的分块矩阵乘法，使用 slice-k 方法，即分块（tile）沿着 K 维度累加所有结果子矩阵。

使用 NVIDIA CuTe 库重写的分块矩阵乘法实现，采用 cute::gemm 期望的标准布局。

2.1. 矩阵布局约定

采用 BLAS/Fortran 风格的列主序 (Column-major)：

Tensor	Shape	Stride	说明
A	(M, K)	(1, M)	列主序，M方向连续
B	(N, K)	(1, N)	列主序，存储 B^T
C	(M, N)	(1, M)	列主序，M方向连续

矩阵参数，以及划分参数：M=1024，N=1024，K=1024*8，BM=64，BN=64，BK=16，TM=8，TN=8。 关键点：B 矩阵以 (N, K) 形式存储，实际上是原始 B(K, N) 的转置。这是 cute::gemm 的标准输入格式。

创建的矩阵 A、B、C 的 tensor 视图如下：

  
// A: (M, K) 列主序, stride = (1, M)
// B: (N, K) 列主序, stride = (1, N)  -- 注意这里存的是B的转置
// C: (M, N) 列主序, stride = (1, M)
Tensor mA = make_tensor(make_gmem_ptr(Aptr), make_shape(M, K), make_stride(Int<1>{}, M));
Tensor mB = make_tensor(make_gmem_ptr(Bptr), make_shape(N, K), make_stride(Int<1>{}, N));
Tensor mC = make_tensor(make_gmem_ptr(Cptr), make_shape(M, N), make_stride(Int<1>{}, M));

kernel 的 dimensions 配置为：

  
dim3 gridDim(N / BN, M / BM);   // (16, 16)
dim3 blockDim(BN / TN, BM / TM);// (8, 8)

2.2. CuTe 实现：分块分割、线程分区、拷贝及计算

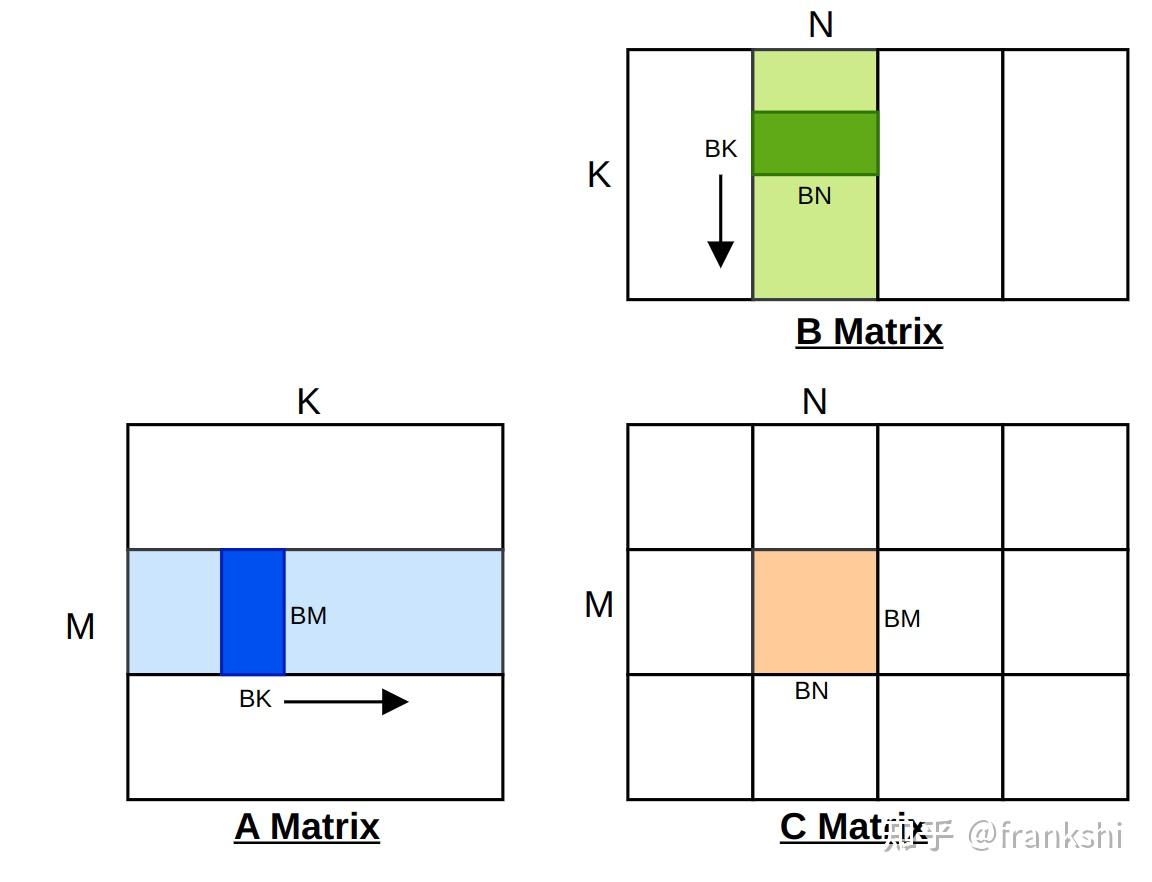
以矩阵 A 为例，矩阵 A 在 M 纬度上，每个 Thread Block 负责处理 BM 行（复制 + GEMM）；在 K 维度上，Thread Block 负责处理 BK 列。Thread Block 以二维的方式划分，需要的 Thread Block 数量为 (M/BM, N/BN)，即划分的 tile 数量；每个 Thread Block 内的线程数量为 (BM/TM, BN/TN)，即同样以二维的方式将 tile 再次划分给 Thread Block 内的线程。

使用 slice-k 方法，Thread Block 需要循环遍历 K 维度，将矩阵 A 分块加载到 SMEM 中。所以创建的 tile tensor 视图是一个三维 tensor： (BM, BK, K/BK) 大小。矩阵 B 同理，得到的三维 tensor：(BN, BK, K/BK)。

由于分块计算得到的 C 矩阵 tile 大小为 (BM, BN)，所以需要取得矩阵 C 的 tile tensor。

矩阵 A、B 分块 GEMM 需要的 SMEM。其本质是缓存，大小为一个 tile 大小。即针对矩阵 A，Thread Block 每次从 GMEM 中依次取得 (BM, BK) 分块大小复制到 SMEM，然后沿着 K 维度循环 for(product)。定义如下：

  
__shared__ T smemA[BM * BK];
__shared__ T smemB[BN * BK];

// sA: (BM, BK) 列主序, stride = (1, BM)
// sB: (BN, BK) 列主序, stride = (1, BN)
Tensor sA = make_tensor(make_smem_ptr(smemA), make_shape(Int<BM>{}, Int<BK>{}), make_stride(Int<1>{}, Int<BM>{}));
Tensor sB = make_tensor(make_smem_ptr(smemB), make_shape(Int<BN>{}, Int<BK>{}), make_stride(Int<1>{}, Int<BN>{}));

2.2.1. 分块操作

  
// 创建全局内存 tensor 视图
Tensor gA = local_tile(mA, make_tile(Int<BM>{}, Int<BK>{}), make_coord(blockIdx.y, _));           // (BM, BK, k)
Tensor gB = local_tile(mB, make_tile(Int<BN>{}, Int<BK>{}), make_coord(blockIdx.x, _));           // (BN, BK, k)
Tensor gC = local_tile(mC, make_tile(Int<BM>{}, Int<BN>{}), make_coord(blockIdx.y, blockIdx.x));  // (BM, BN)

按照语义理解，A 矩阵使用 shape(BM, BK) 沿着 M 维度以及 K 维度进行切分，即将其划分为若干 tile，每个 tile 的大小为 (BM, BK)。而后，使用 make_coord(blockIdx.y, _) 取得第 blockIdx.y 个 tile，在 K 维度上使用 _ 表示取所有 tile，所以生成了一个三维的 Tensor。由于 A 矩阵在 K 维度上被切分为多个 tile，所以最终生成的 tensor 维度为 (BM, BK, K/BK)，即表示有 K/BK 个二维 tile(BM, BK)。

作为对比，矩阵 C 在 M 维度以及 N 维度上进行切分，得到若干个 tile，每个 tile 的大小为 (BM, BN)。而后使用完整的二维坐标 make_coord(blockIdx.y, blockIdx.x) 取得唯一的 tile，故其生成的 tensor 维度为 (BM, BN)。

分块之后，每个 Thread Block 分到的 tile shape 如下：

gA(64, 16, 512)：其中，1024*8 / 16 = 512，即这是一个 tile group
gB(64, 16, 512)：其中，1024*8 / 16 = 512，即这是一个 tile group
gC(64, 64)

2.2.2. 线程分区

分区复制 GMEM -> SMEM：

前面已经按照 Thread Block 分块得到 tile，现在需要继续将划分细化到 Thread Block 内的每个线程。首先计算线程数量：

  
// 线程块配置: (BN/TN, BM/TM) = (8, 8) = 64 线程
constexpr int num_threads = (BM / TM) * (BN / TN);

  
// 线程划分方法：按照 M 维度划分 A 矩阵，N 维度划分 B 矩阵
Layout tA_copy = make_layout(make_shape(Int<num_threads>{}, Int<1>{}));
Layout tB_copy = make_layout(make_shape(Int<num_threads>{}, Int<1>{}));

// 得到本线程划分的 sub-tile
Tensor tAgA = local_partition(gA, tA_copy, tid);  // 每个线程负责的gA部分
Tensor tAsA = local_partition(sA, tA_copy, tid);  // 每个线程负责的sA部分
Tensor tBgB = local_partition(gB, tB_copy, tid);  // 每个线程负责的gB部分
Tensor tBsB = local_partition(sB, tB_copy, tid);  // 每个线程负责的sB部分

针对 tile A，只在 M 维度上进行线程划分，每个线程负责复制 BM / num_threads 行数据，在 K 维度上负责复制全部 K 列数据，维度信息保持，tAgA、tBgB 还是一个三维 tensor。每个线程在执行复制时，在 K 维度上每次复制 BK 列，一共需要 K / BK 次循环，才能完成 sub-tile 的加载以及 GEMM 得到最终的结果。

矩阵 B 同理，只在 N 维度上进行线程划分。

得到的线程分区 tensor layout 如下：

tAgA(1, 16)：shape: (_1,_16,512), stride: (_0,1024,16384)
tAsA(1, 16)：shape: (_1,_16), stride: (_0,64)
tBgB(1, 16)：shape: (_1,_16,512), stride: (_0,1024,16384)
tBsB(1, 16)：shape: (_1,_16), stride: (_0,64)

计算分区：

每个线程复制划分，是针对矩阵 A、B 进行的。计算 C 矩阵时，需要取得 A(TM, TK) 分块、B(TN, TK) 分块、C(TM, TN)，进行线程分块的 GEMM 计算。复制时的线程分块与计算时的线程分块可以分开，因为在 GMEM -> SMEM 复制之后，使用 __syncthreads 保证 Thread Block 的 A-tile、B-tile 都完成复制（更严谨的说，是在 GMEM -> SMEM 与 sub-tile GEMM 两个步骤之间同步）。

  
// 计算时的线程划分方法: (BM/TM, BN/TN) = (8, 8)
Layout tC = make_layout(make_shape(Int<BM / TM>{}, Int<BN / TN>{}));

// local_partition: 按线程布局分配工作
// Step<_1, X> 表示第 0 维参与分区，第 1 维不参与
Tensor tCsA = local_partition(sA, tC, tid, Step<_1, X>{});   // (TM, BK)
Tensor tCsB = local_partition(sB, tC, tid, Step<X, _1>{});   // (TN, BK)
Tensor tCgC = local_partition(gC, tC, tid, Step<_1, _1>{});  // (TM, TN)

线程分区之后，得到的每个线程的 tensor layout 如下：

  
tCsA shape: (_8,_16), stride: (_8,_64)
tCsB shape: (_8,_16), stride: (_8,_64)
tCgC shape: (_8,_8), stride: (_8,8192)

2.2.3. slice-k GEMM

  
// 遍历K维度
const int num_tile_k = K / BK;
for (int k = 0; k < num_tile_k; k++) {
  // 从全局内存复制到共享内存
  copy(tAgA(_, _, k), tAsA);
  copy(tBgB(_, _, k), tBsB);

  __syncthreads();  // 等待所有线程完成复制

  // 使用 cute::gemm 执行矩阵乘法
  // gemm 期望: A(M,K), B(N,K), C(M,N) - B是(N,K)形式
  gemm(tCsA, tCsB, tCrC);  // tCrC += tCsA * tCsB^T

  __syncthreads();  // 等待所有线程完成计算
}

在 tile 分区的时候，已经将 A-tile、B-tile 划分为 K/BK 个子 tile，即沿着 K 维度进行了分块。计算时，针对每一个 sub-tile 进行 GEMM，一共迭代 K / BK 次。

当矩阵是列主序时（比如矩阵 A、B 是 K-major），如果 Thread Block 内的线程任务划分也按照 K-major 进行，这样得到的访问矩阵内的元素的编号也是连续的，即访存合并。

2.2.4. Bank Conflict 计算

依据 outter-partition 划分的方式：

  
Layout tC = make_layout(make_shape(Int<BM / TM>{}, Int<BN / TN>{}));

Tensor tCsA = local_partition(sA, tC, tid, Step<_1, X>{});   // (TM, BK)
Tensor tCsB = local_partition(sB, tC, tid, Step<X, _1>{});   // (TN, BK)

线程在 tC layout 中的二维坐标：

tC_row = tid % 8  (M 维度方向)
tC_col = tid / 8  (N 维度方向)

2.2.4.1. tCsA 访问方式及 bank conflict 分析

Step<_1, X> 表示使用 M 维度参与分区。

线程的 tCsA 起始行号为：

\[\mathrm{row\_offset}_{A} = \mathrm{tC\_row} \times \mathrm{TM} = (\mathrm{tid} \mod 8) \times 8\]

线程访问 sA 的地址计算公式：

\[\begin{aligned} & \mathrm{addr}_{sA}[m, k] = (\mathrm{row\_offset}_{A} + m) + k \times 64 \\ & m \in [0, 7], k \in [0, 15] \end{aligned}\]

stride=8，可以理解为每个线程占据 8 个float 类型数据，则 4 个线程之后即产生 bank conflict。

此时，每隔 4 个线程，访问的地址会落在同一个 bank 上，并产生 bank conflict。一个 warp 内（tid - bankId）对应表如下：

[0 -  0,   1 -  8,   2 -  16,    3 - 24]
[4 -  0,   5 -  8,   6 -  16,    7 - 24]
[8 -  0,   9 -  8,   10 - 16,   11 - 24]
[12 - 0,   13 - 8,   14 - 16,   15 - 24]

其中，由于 m = (m+1) % 8，第 8 个线程地址跳跃 64 个 float。

即一个 warp 产生 4 个 4-way bank conflict。

2.2.4.2. tCsB 访问方式及 bank conflict 分析

Step<X, _1> 表示使用 N 维度参与分区。

每个线程的 tCsB 起始行号为：

\[\mathrm{row\_offset}_{B} = \mathrm{tC\_col} \times \mathrm{TN} = \lfloor \mathrm{tid} / 8 \rfloor \times 8\]

线程访问 sB 的地址计算公式：

\[\begin{aligned} & \mathrm{addr}_{sB}[n, k] = (\mathrm{row\_offset}_{B} + n) + k \times 64 \\ & n \in [0, 7], k \in [0, 15] \end{aligned}\]

此时，每 8 个线程一组，其访问地址都是同一个地址。下一组 8 个线程，其在 smemB[] 中的编号 +8。即每相邻的 8 个线程，产生一个 broadcast。对应表格如下：

[0 - 0,  1 - 0,  2 - 0,  3 - 0, 4 - 0,  5 - 0,  6 - 0,  7 - 0]
[8 - 8,  9 - 8,  10 -8,  11 -8, 12 -8,  13 -8,  14 -8,  15 -8]

一个 warp 内，从第 8 个线程开始，访问编号跳转了 64 个 float。

2.2.4.3. 总结

发现，在当前情况下（sA 与 sB 布局相同，且划分大小相同），他们之前不一样的地方，来自于划分时，选择的维度不同：

首先，线程被划分为两个维度，且使用这两个维度分别去划分 sA 与 sB。
其次，由于使用了这两个维度进行划分，导致 M 维度是使用取余，N 维度是使用整除。这才是导致访问模式不同的根本原因。

性能影响：

tCsA 访问产生 bank conflict，影响性能。
tCsB 访问产生 broadcast，带宽利用率低。

2.3 Stride 理解

make_stride(s0, s1) 定义了沿各维度移动时的内存跳跃距离：

stride(1, M) → 第0维步长=1（连续），第1维步长=M → 列主序
stride(M, 1) → 第0维步长=M，第1维步长=1（连续） → 行主序

简单记忆：Stride 为 1 的维度在内存中连续。

2.4 CuTe 命名约定

CuTe 官方推荐的变量命名规则，便于理解代码中各 tensor 的用途和存储位置。

前缀含义：

前缀	英文	含义
`m`	matrix	完整矩阵的 tensor 视图
`g`	global	全局内存中的 tile
`s`	shared	共享内存中的 tensor
`r`	register	寄存器中的 tensor
`t`	thread	线程级别的分区/布局

后缀含义：

后缀	含义
`A`	矩阵 A 相关
`B`	矩阵 B 相关
`C`	矩阵 C 相关

组合命名规则 tXyZ：

t = thread 级别
X = 用于什么操作（A=复制A, B=复制B, C=计算C）
y = 存储位置（g=global, s=shared, r=register）
Z = 哪个矩阵（A, B, C）

示例：

  
Tensor mA = ...;     // matrix A - 完整矩阵视图
Tensor gA = ...;     // global A - 全局内存中的 tile
Tensor sA = ...;     // shared A - 共享内存 tensor

Tensor tAgA = ...;   // thread partition (for A copy) of global A
Tensor tAsA = ...;   // thread partition (for A copy) of shared A
Tensor tCsA = ...;   // thread partition (for C compute) of shared A
Tensor tCrC = ...;   // thread partition (for C compute) of register C

为什么同一个矩阵有不同的分区？ 因为复制和计算时的线程分工不同。例如 sA：复制时：64个线程平均分配 BM×BK 元素 → tAsA 计算时：每个线程取 TM×BK 子矩阵 → tCsA

资料

Matrix Multiplication Background User’s Guide。如何计算 GEMM 的性能指标
CuTe dense matrix-matrix multiply tutorial。CuTe GEMM 官方 Document。
reed – cute 之简单GEMM实现
reed – cute 之 MMA抽象
Mao Lei – CuTe Local Partition

CUDA

本文由作者按照 CC BY 4.0 进行授权