随机一致性抽样算法（RANSAC）

1. RANSAC 算法过程

最小二乘法拟合只进行一次迭代，计算所有离散点平均值，得到最终拟合直线或曲线。

RANSAC通过多次迭代，寻找拟合直线或曲线的最佳（最近）权重的点。第N次拟合，得到第N次迭代的内点（集合）。第N+1次迭代，得到第N+1次的内点（集合），如果第N+1次迭代计算的内点其权重大于第N次迭代的内点的权重，则更新最佳内点为第N+1次的内点（集合）。

其入参有：

• 点集；
• 拟合误差delta，作为判断内点的阈值；
• 迭代次数loopNum；

其计算流程为：

1. 随机选取一个点作为起点，随机选取另一个点作为终点；
2. 从集合中查找所有误差在delta范围内的点集合：作为本次内点（集合）：this_inlier，计算其权重，与保存的权重比较best_weight，如果本次权重较好，则更新best_inlier为本次内点（集合），且更新best_weight为本次权重；
3. 标记本次循环所访问过的点：包括终点在内的this_inlier为visited状态，后面的迭代中不再访问这些点；
4. 重复步骤2-4，直到达到设定的迭代次数loopNum；

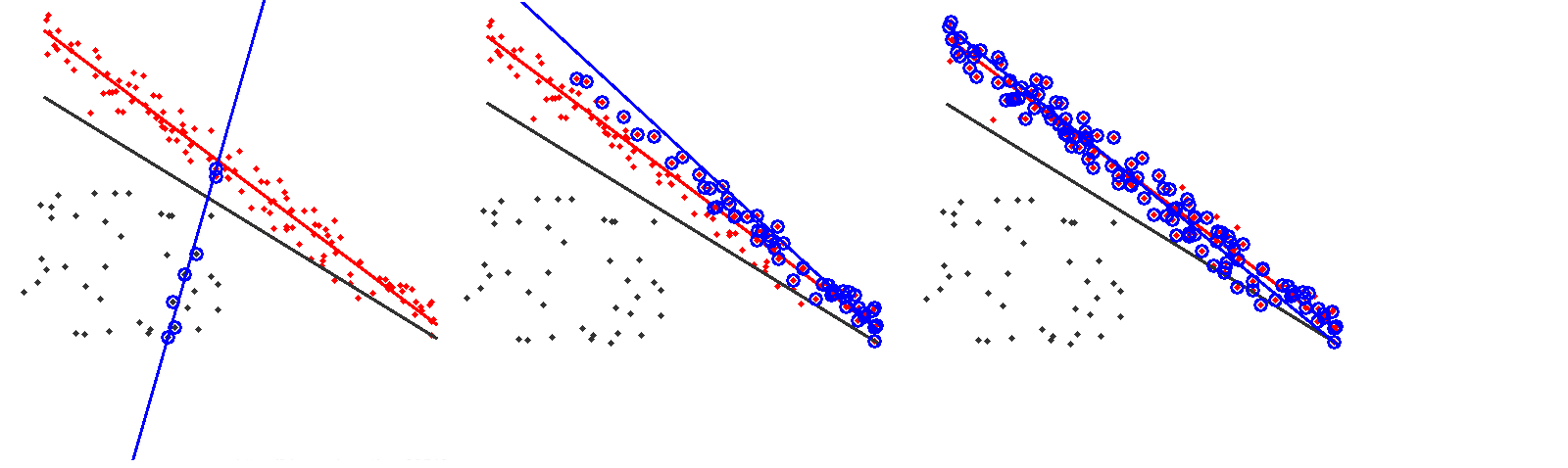
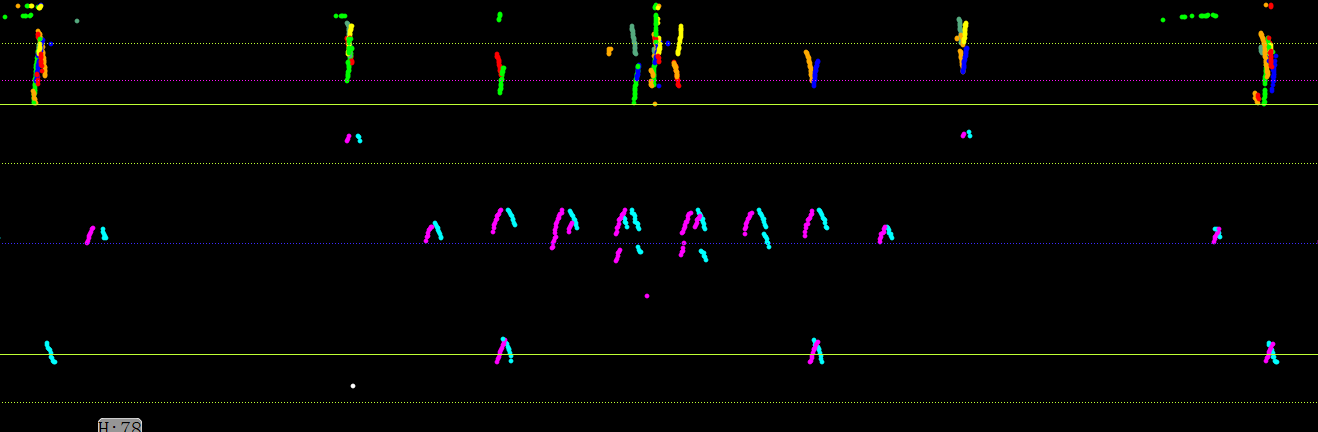
Demo计算结果如下：

2. 算法改进

实际应用中，发现不能直接应用RANSAC算法。一个原因离散点（点云）数量过大，实际应用不能拟合期望的直线。另外就是其迭代次数在大数据量下，计算量过大。

改进措施包括：

1. 通过其他分块算法，初步得到拟合线段所在区域；
2. 根据行业应用特点，限定起点、限定密度、限定斜率；
3. 综合使用其中一个或多个，特别是初步筛选及限定起点；

3. 实现

TBD

4. 更多资料

• Ransac 随机一致性采样