文章

OpenCascade拓扑与几何的关系

发表于 更新于
作者 Roderick.Huang 7 分钟阅读

1. OPENCASCADE 中的拓扑结构（TopoDS包）

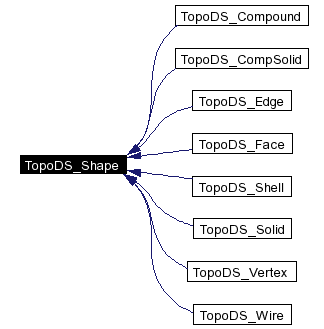
抽象结构是以TopoDS包的C++类来实现的。下面是一个继承图，取自Doxygen生成的文档。

TopoDS_inheritance_diagram

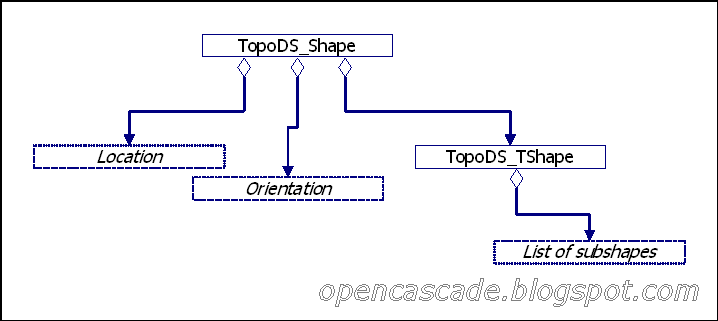
TopoDS_Shape 是通过值来操作的，包含3个字段–location、orientation 和一个 myTShape 句柄 （TopoDS_TShape类型），见下图（只包含最重要的字段）：

TopoDS_Shape_structure_diagram

myTShape 和 Location 被用来在各种形状之间共享数据，从而节省大量的内存。例如，两个连接在一起的面中间的边，这个边具有相同的位置（location）和 myTShape，但有不同的朝向（orientation）（在其中一个面是正向，在另一个面中是反向）。

2. OPENCASCADE 中的边界表示法（BRep包）

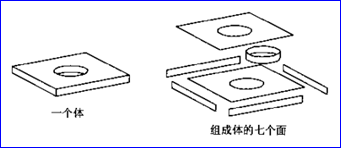
边界表示（Boundary Representation）也称为BRep表示，它是几何造型中最成熟、无二义的表示法。实体的边界通常是由面的并集表示，而每个面又由它所在曲面的定义加上其边界来表示，面的边界是边的并集，而边又是由点来表示。如下图1.1所示，曲面的汇合处形成曲线，而曲线的汇合处形成点。所以点、线、面是描述一个形状所需要的基本组成单元。

BRep Shape demo

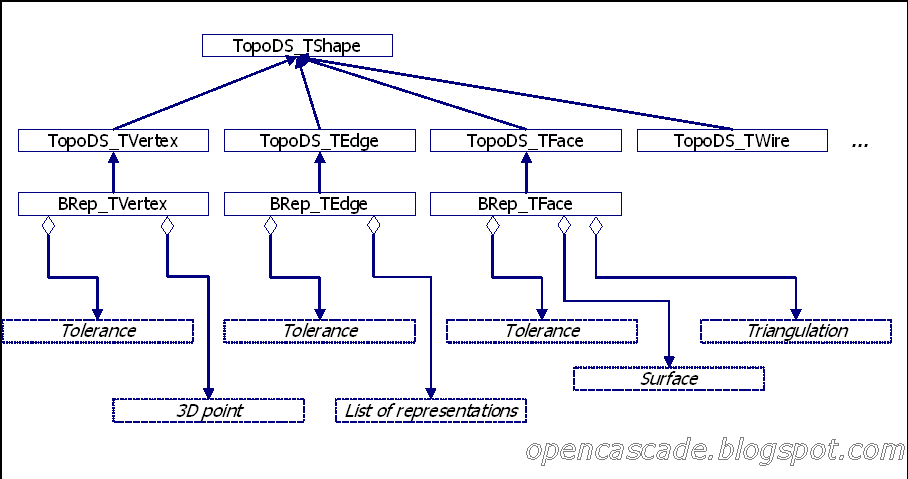
几何信息（在BRep包中）通过继承TopoDS_Shape类来实现，只有3种类型的拓扑对象有几何特征–顶点（vertex）、边(edge)和面(face)（见下图）：

BRep_Shape_inheritance_diagram

2.1 Brep 进一步说明

几何信息（BRep）描述了形状的形状、位置、方向、边界等信息，而拓扑信息（TopoDS）描述了形状的拓扑结构，如顶点、边、面的连接关系。以BRep Edge为例说明： 边有几种几何表示方式（参考上图，BRep_TEdge之下有节点List of Edge Representions）:

  • 三维空间的曲线C(t)，用类Geom_Curve实现，这是基础表示方式。
  • 曲线P(t)为二维空间中的参数曲线，用于描述位于曲面上的曲线。这些通常被称为pcurves，用类Geom2d_Curve实现。
  • 多边形（Polygonal representation）用一组三维点来描述，用类Poly_Polygon3D实现。
  • 多边形（Polygonal representation），也可以用一组三维点的编号来描述，在类Poly_PlygonOnTriangulation实现。

3. OpenCascade 中拓扑（Topo）与几何（BRep）的关系

边界表示的一个重要特点是描述形状的信息包括几何信息（geometry）和拓朴（topology）信息两个方面：

  1. 拓朴信息描述形状上的顶点、边、面的连接关系，它形成物体边界表示的“骨架”。
  2. 形状的几何信息犹如附着在“骨架”上的肌肉。在OpenCascade中，形状的几何信息包含曲线和曲面的参数解析表示Geom_Curve/Geom_Surface。

这样我们就可以用平面方程和柱面方程来描述曲面，用直线或圆弧方程来描述曲线。这时会出现一个问题，即代数表达式只能定义无边界的几何体。除了单个点、圆以及球体，经典的解析几何仅能表示无限延伸的曲线和曲面。为了解决这个问题，边界表示法按下述方法明确地定义曲线或曲面的边界：

  • 曲线的边界由位于曲线上的一对点来确定；
  • 曲面的边界由位于曲面上的一组曲线来确定；

通过这个方法，就可以定义一段曲线或一片曲面。这时，不同几何元素之间的关系的组织问题就出现了，为此我们将记录如下信息：

  • 哪些点界定哪些曲线；
  • 哪些曲线界定哪些曲面；

这些关于谁关联谁的信息，就是几何造型系统经常提到的拓朴。在边界表示法中，理论上表示一个物理模型只需要三个拓朴体（顶点TopoDS_Vertex、边TopoDS_Edge和面TopoDS_Face），但在实际应用中，为了提高计算机处理的速度或提供高级的操作功能，还要引入其他一些概念，如环TopoDS_Wire、壳TopoDS_Shell、复合体TopoDS_Compound等。

z. 原文及参考

z.1 ROMAN LYGIN

在occ dev上对应的讨论帖子：

z.2 国内 eryar 等同文章系列

eryar 其他相关文章及代码：

z.3 ROMAN LYGIN 原文的中文翻译

z.4 其他资料

OCCT
occt
本文由作者按照 CC BY 4.0 进行授权