文章

聚类算法（密度）：基于 nano-flann

发表于 更新于
作者 Roderick.Huang 7 分钟阅读

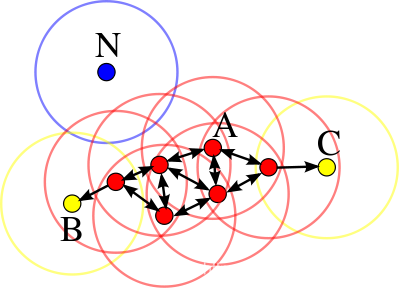
0. DBSCAN 算法及 K-D 树介绍

DBSCAN算法相关概念：

  1. 邻域半径 eps。
  2. 核心点，最少核心点 minPts。
  3. 直接密度可达。
  4. 密度可达。
  5. 密度相连。

DBSCAN 密度概念

K-D树的时间复杂度：

Kdtree 算法的构建时间复杂度为 O(nlogn)，搜索时间复杂度最好为 O($\log_2 N$)，最坏为 O($N^{1-1/k}$)。

1. 背景

采集到的二维点云数据(samples)，生成K-D搜索树，使用广度优先搜索，聚合成block数据。后续的识别/分类算法，在block数据基础上进行。

由于使用点云处理库PCL比较庞大，以及其依的FLANN基于C++14，使用C++17/20导致在自定义点云数据结构时，编译有些STL算法库被废弃，编译出错。故使用 nanoflann。

2. 基于 nano-flann 的聚类算法实现

2.1 自定义点云数据结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

#pragma once
// test\test_flann\flann_adaptor.h

#include <vector>

#include "3rd_utils.h"
#include "typedef.h"

struct PointCloud {
  using Point = rias::data_type::sample_data_t;
  using coord_t = double;  //!< The type of each coordinate

  std::vector<Point> pts;

  // Must return the number of data points
  inline size_t kdtree_get_point_count() const { return pts.size(); }

  // Returns the dim'th component of the idx'th point in the class:
  // Since this is inlined and the "dim" argument is typically an immediate
  // value, the
  //  "if/else's" are actually solved at compile time.
  inline double kdtree_get_pt(const size_t idx, const size_t dim) const {
    CHECK2(dim < 2, "Invalid dimension: " << dim);
    if (dim == 0) return pts[idx].mapped_pos_.x_;
    else return pts[idx].mapped_pos_.y_;
  }

  // Optional bounding-box computation: return false to default to a standard
  // bbox computation loop.
  //   Return true if the BBOX was already computed by the class and returned
  //   in "bb" so it can be avoided to redo it again. Look at bb.size() to
  //   find out the expected dimensionality (e.g. 2 or 3 for point clouds)
  template <class BBOX>
  bool kdtree_get_bbox(BBOX& /* bb */) const {
    return false;
  }
};

2.2 基于 K-D 树构建广度优先搜索算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101

#pragma once
// test\test_flann\point_cloud_algorithm.h

#include <queue>
#include <vector>

#pragma warning(push)
#pragma warning(disable : 4267)  // disable conversion warning
#include "nanoflann/nanoflann.hpp"
#pragma warning(pop)

#include "3rd_utils.h"

#include "flann_adaptor.h"
#include "typedef.h"

namespace rias::test {

class BFSDensitySampleSearch {
  static constexpr int32_t kDIM = 2;
  using my_kd_tree_t = nanoflann::KDTreeSingleIndexAdaptor<nanoflann::L2_Simple_Adaptor<double, PointCloud>, PointCloud, kDIM>;
  using sample_t = rias::data_type::sample_data_t;

 public:
  BFSDensitySampleSearch(const std::vector<sample_t>& pts) : pts_(pts) {}
  ~BFSDensitySampleSearch() = default;

  BFSDensitySampleSearch& setRadius(double radius) {
    radius_ = radius;
    return *this;
  }

  BFSDensitySampleSearch& setMinPts(double minPts) {
    minPts_ = minPts;
    return *this;
  }

  const std::vector<std::vector<size_t>>& clusters() const { return clusters_; }

  BFSDensitySampleSearch& search() {
    PointCloud cloud;
    cloud.pts = pts_;

    CHECK1(sizeof(double[kDIM]) == sizeof(data_type::point_double_t), "sizeof(double[kDIM])");
    my_kd_tree_t index(kDIM /*dim*/, cloud, {10 /* max leaf */});
    std::vector<double> densities(pts_.size(), double{});

    for (size_t i = 0; i < pts_.size(); i++) {
      const auto* q_pt = (double*)(&pts_[i].mapped_pos_);
      std::vector<nanoflann::ResultItem<uint32_t, double>> ret_matches;
      const size_t n_matched = index.radiusSearch(q_pt, radius_, ret_matches);
      densities[i] = static_cast<double>(n_matched);
    }

    std::vector<bool> visited(pts_.size(), false);
    for (size_t i = 0; i < pts_.size(); i++) {
      if (visited[i] /*|| densities[i] < minPts_*/) {  // 0. skip visited or low density points
        continue;
      }

      std::vector<size_t> cluster;
      std::queue<size_t> q;

      q.push(i);  // 1. add self ot queue at first
      visited[i] = true;

      while (!q.empty()) {
        const auto idx = q.front();
        q.pop();

        cluster.push_back(idx);  // 2. elements in the same queue are in the same cluster

        const auto* q_pt = (double*)(&pts_[idx].mapped_pos_);
        std::vector<nanoflann::ResultItem<uint32_t, double>> ret_matches;
        const size_t n_matched = index.radiusSearch(q_pt, radius_, ret_matches);

        for (size_t j = 0; j < n_matched; j++) {  // 3. add matched points to the same queue
          const auto n_idx = ret_matches[j].first;
          // const auto n_dist = ret_matches[j].second;
          if (!visited[n_idx] && densities[n_idx] >= minPts_) {
            visited[n_idx] = true;
            q.push(n_idx);
          }
        }
      }

      // 4. a cluster done (one or more points)
      clusters_.push_back(cluster);
    }

    return *this;
  }

 private:
  const std::vector<sample_t>& pts_;
  double radius_{1.0}, minPts_{1.0};

  std::vector<std::vector<size_t>> clusters_;
};

}  // namespace rias::test

2.3 测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

{
    const auto t0 = std::chrono::high_resolution_clock::now();

    auto dss = BFSDensitySampleSearch(sample_ds->ds_).setRadius(3.0).setMinPts(1.0);
    auto clusters = dss.search().clusters();

    const auto t1 = std::chrono::high_resolution_clock::now();
    const auto dur = std::chrono::duration<double, std::milli>(t1 - t0).count();
    spdlog::info("search in {} points. found {} clusters. time: {:.3f} seconds\n", sample_ds->ds_.size(), clusters.size(),
                 dur / 1000.0);

    /*for (const auto& cluster : clusters) {
      //spdlog::info("{}", fmt::join(cluster, ", "));
      spdlog::info("cluster: {}", cluster);
    }*/
}

2.4 测试

1
2
3
4

[2024-08-26 21:47:35.648] [warning] [dataxy_loader.cc:146] under flow 870 samples in dataset
[2024-08-26 21:47:35.649] [info] load data from file: 0.37393689999999996 seconds

[2024-08-26 21:47:37.740] [info] search in 1503894 points. found 438931 clusters. time: 2.133 seconds

TODO: 测试小数据集下的性能对比。

2.5 参考

3. 基于templated的聚类算法实现(线性搜索 O2时间复杂度)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

template <typename ElemType, typename LinerFuncType, typename AdjFuncType>
class BFSLinerMerge {
 public:
  BFSLinerMerge(const std::vector<ElemType>& blocks, LinerFuncType linerCondFunc, AdjFuncType adjCondFunc)
      : blocks_(blocks), liner_cond_func_(linerCondFunc), adj_cond_func_(adjCondFunc) {};

  BFSLinerMerge& search() {
    if (!clusters_.empty()) clusters_.clear();
    std::vector<bool> visited(blocks_.size(), false);
    clusters_.reserve(blocks_.size());

    for (size_t i = 0; i < blocks_.size(); i++) {
      if (visited[i]) continue;

      std::queue<size_t> q;
      q.push(i);
      visited[i] = true;

      std::vector<Block*> cluster;
      while (!q.empty()) {
        size_t idx = q.front();
        q.pop();

        const auto this_blk = blocks_[idx];
        cluster.push_back(blocks_[idx]);

        for (size_t j = 0; j < blocks_.size(); j++) {
          if (visited[j]) continue;

          const auto& blkj = blocks_[j];
          if (liner_cond_func_(this_blk, blkj) && adj_cond_func_(this_blk, blkj)) {
            q.push(j);
            visited[j] = true;
          }
        }
      }

      clusters_.push_back(cluster);
    };

    return *this;
  }

  std::vector<std::vector<ElemType>>& clusters() { return clusters_; }

 private:
  const std::vector<ElemType>& blocks_;
  LinerFuncType liner_cond_func_;
  AdjFuncType adj_cond_func_;

  std::vector<std::vector<ElemType>> clusters_;
};

4. 聚类算法资料收集

algorithm
algorithm cpp
本文由作者按照 CC BY 4.0 进行授权